해당 포스팅은 <밑바닥부터 시작하는 딥러닝1> 책을 기준으로 하며, 공부 기록 목적으로 작성되었습니다.

학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻한다. 손실 함수는 신경망이 학습할 수 있도록 해주는 지표로 손실 함수의 결괏값을 가장 작게 만드는 개중치 매개변수를 찾는 것이 학습의 목표이다.
데이터에서 학습한다!
신경망의 특징은 데이터를 보고 학습할 수 있다는 점이고 학습한다는 것은 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 의미이다.
데이터 주도 학습
기계학습은 데이터에서 답과 패턴을 찾고 데이터로 이야기를 만드는 것이기 때문에 그 중심에는 데이터가 존재한다.
기계학습에서는 사람의 개입을 최소화하고 수집한 데이터로부터 패턴을 찾으려 시도한다. 신경망과 딥러닝은 기존 기계학습에서 사용하던 방법보다 사람의 개입을 더욱 배제할 수 있게 해주는 중요한 특정을 지녔다.
이미지에서 특징을 추출하고 그 특징의 패턴을 기계학습의 기술로 학습하는 방법이 있다. 여기서 말하는 특징은 입력 데이터에서 본질적인(중요한) 데이터를 정확하게 추출할 수 있도록 설계된 변환기를 가리킨다. 이미지의 특징은 보통 벡터로 기술하고, 컴퓨터 비전 분야에서는 SIFT, SURF, HOG 등의 특징을 많이 사용한다. 이런 특징을 사용하여 이미지 데이터를 벡터로 변환하고 변환된 벡터를 가지고 지도 학습 방식의 대표 분류 기법인 SVM, KNN 등으로 학습할 수 있다.
기계학습에서는 데이터로부터 규칙을 찾는 역할을 '기계'가 담당하지만, 이미지를 벡터로 변환할 때 사용하는 특징은 여전히 '사람'이 설계한다 문제에 적합한 특징을 쓰지 않으면 좋은 결과를 얻을 수 없다.
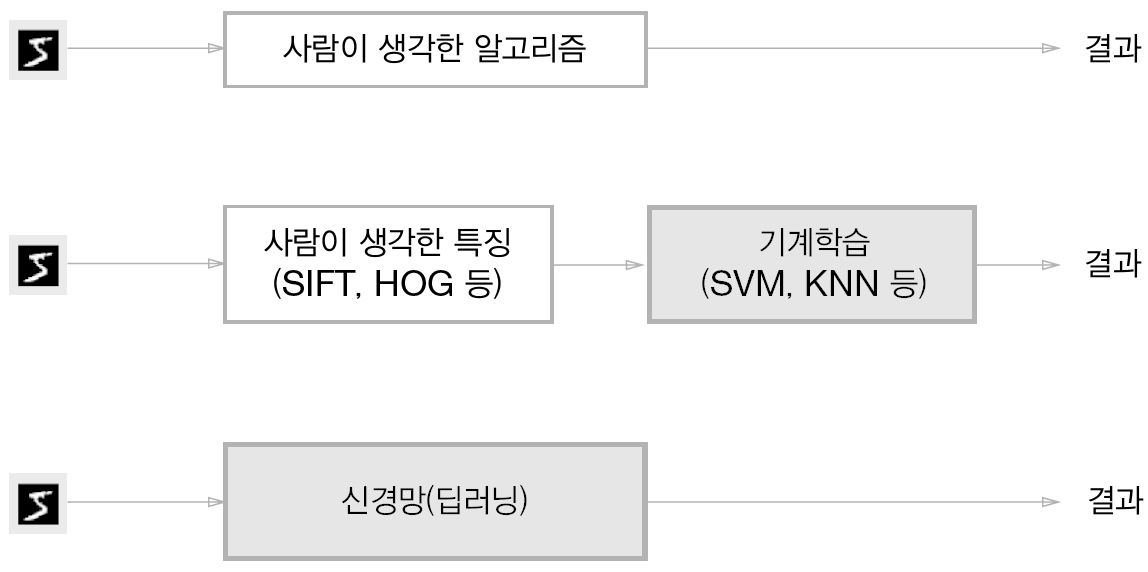
신경망은 이미지는 있는 그대로 학습하기 때문에 두 번째 접근 방식에서는 특징을 사람이 설계했지만, 신경망은 이미지에 포함된 중요한 특징까지도 기계가 스스로 학습한다.
훈련 데이터와 시험 데이터
기계학습 문제는 데이터를 훈련 데이터와 시험 데이터로 나눠 학습과 실험을 수행한다. 우선 훈련 데이터만 사용하여 학습하면서 최적의 매개변수를 찾고 시험 데이터를 사용하여 앞서 훈련한 모델의 실력을 평가한다.
훈련, 시험 데이터를 나누는 이유?
우리는 범용적으로 사용할 수 있는 모델을 원하는데 이 범용 능력을 제대로 평가하기 위해서 데이터를 분리하는 것이다.
범용 능력은 아직 보지 못한 데이터로 문제를 올바르게 풀어내는 능력으로 범용 능력 획득이 기계학습의 최종 목표이다.
한 데이터셋에만 지나치게 최적화된 상태를 오버피팅이라고 하는데, 오버피팅을 피하는 것이 기계학습의 중요한 과제 중 하나이다.
손실 함수
신경망 학습에서는 현재의 상태를 하나의 지표로 표현한다. 그리고 그 지표를 가장 좋게 만들어주는 가중치 매개변수의 값을 탐색한다. 신경망 학습에서 사용하는 지표를 손실함수라고 하며 일반적으로 오차제곱합과 교차 엔트로피 오차를 사용한다.
오차제곱합
가장 많이 쓰이는 손실 함수는 오차제곱합(sum of squares for error, SSE)으로 수식은 다음과 같다.
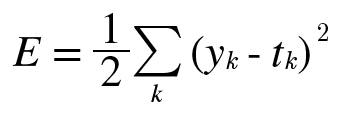
여기서 yk는 신경망의 출력(신경망이 추정한 값), tk는 정답 레이블, k는 데이터의 차원 수를 나타낸다. 신경망 출력 y는 소프트맥스 함수의 출력이 된다.
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)교차 엔트로피 오차
교차 엔트로피 오차(cross entropy error, CEE,)도 자주 이용한다. 수식은 다음과 같다.
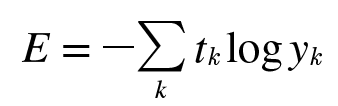
yk는 신경망 출력, tk는 정답 레이블이다. tk는 정답에 해당하는 인덱스의 원소만 1이고 나머지는 0이다(원-핫 인코딩). 실질적으로 정답일 때의 추정(tk가 1일 때의 yk)의 자연로그를 계산하는 식이 된다. 즉, 교차 엔트로피 오차는 정답일 때의 출력이 전체 값을 정하게 된다.
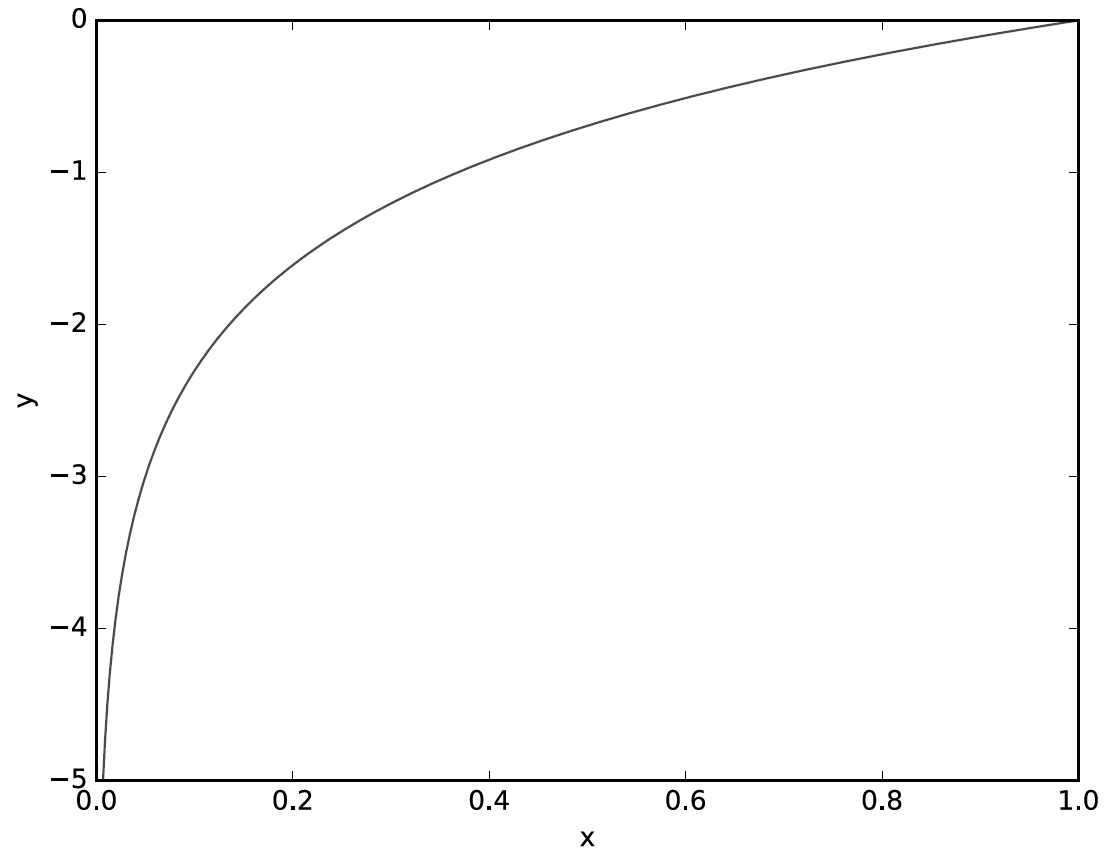
자연로그의 그래프는 위 그림에서 보듯이 x가 1일 때 y는 0이 되고 x가 0에 가까워질수록 y 값의 점점 작아진다. 교차 엔트로피 오차의 식도 마찬가지로 정답에 해당하는 출력이 커질수록 0에 다가가다가, 그 출력이 1일 때 0이 됩니다. 반대로 정답일 때의 출력이 작아질수록 오차는 커집니다.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))여기서 y와 t는 넘파이 배열이다. np.log() 함수에 0을 입력하면 마이너스 무한대를 뜻하는 -inf가 되어 더 이상 계산을 진행할 수 없게 되기 때문에 아주 작은 값 delta를 더에서 절대 0이 되지 않도록 했다.
미니배치 학습
기계학습 문제는 훈련 데이터를 사용해 학습하기 때문에 모든 훈련 데이터에 대해 손실 함수 값을 구해야 하고, 모든 손실 값의 합을 지표로 삼는다. 식은 다음과 같다.
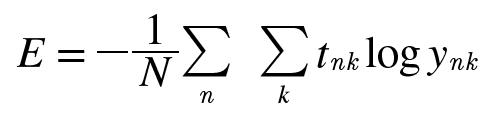
데이터가 N개라면 tnk는 n번째 데이터의 k번째 값을 의미한다(ynk는 신경망의 출력, tnk는 정답 레이블). 마지막에 N으로 나누어 정규화하고 있으며 N으로 나눔으로써 평균 손실 함수를 구한다.
데이터가 아주 많을 경우 데이터 일부를 추려 전체의 근사치로 이용할 수 있다. 신경망 학습에서도 훈련 데이터로부터 일부만 골라 학습을 수행하는데 이 일부를 미니배치라고 하고 이러한 학습 방법을 미니배치 학습이라고 한다.
훈련 데이터에서 지정한 수의 데이터를 무작위로 골라내는 코드는 다음과 같다.
import sys, os
sys.path.append("./dataset")
import numpy as np
import pickle
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize = False)
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
np.random.choice(60000, 10)
# array([20705, 1907, 45562, 31219, 25882, 2401, 22636, 14447, 2463, 17281])손실 함수도 미니배치로 계산할 수 있다.
(배치용) 교차 엔트로피 오차 구현하기
미니배치 같은 배치 데이터를 지원하는 교차 엔트로피 오차는 아래 코드와 같이 구현할 수 있다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7) / batch_size)y는 신경망의 출력, t는 정답 레이블이다. y가 1차원이라면 즉, 데이터 하나당 교차 엔트로피 오차를 구하는 경우는 reshape 함수로 데이터의 형상을 바꿔준다. 그리고 배치의 크기로 나눠 정규화하고 이미지 1장 당 평균의 교차 엔트로피 오차를 계산한다.
정답 레이블이 원-핫 인코딩이 아니라 숫자 레이블로 주어졌을 때의 교차 엔트로피 오차는 다음과 같이 구현 가능하다.
def cross_entropy_error2(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y[np.arange(batch_size), t] + 1e-7) / batch_size)이 구현에서는 원-핫 인코딩일 때 t가 0인 원소는 교차 엔트로피 오차도 0이므로, 그 계산은 무시해도 좋다는 것이 핵심이다. 즉, 정답에 해당하는 신경망 출력만으로 교차 엔트로피 오차를 계산할 수 있다는 것이다.
왜 손실 함수를 설정하는가?
정확도라는 지표를 놔두고 손실 함수의 값이라는 우회적인 방법을 택하는 이유는 뭘까?
신경망 학습에서는 최적의 매개변수를 탐색할 때 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾는다. 이때 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다. 그러나 미분 값이 0이면 손실 함수의 값이 줄어들지 않고 가중치 매개변수의 갱신이 멈춘다. 정확도를 지표로 삼아서 안 되는 이유는 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없기 때문이다.
정확도는 매개변수의 미소한 변화에는 거의 반응을 보이지 않고, 반응이 있더라도 그 값이 불연속적으로 갑자기 변화한다.. 한편 손실 함수는 연속적으로 변화한다.
이는 계단 함수를 활성화 함수로 사용하지 않는 이유와도 들어맞는다. 매개변수의 작은 변화를 계단 함수가 말살하여 손실 함수의 값에 아무런 변화가 나타나지 않기 때문이다. 시그모이드 함수는 출력이 연속적이고 기울기도 연속적으로 변화하여 어느 장소를 미분해도 0이 되지 않는다. 이 성질이 신경망이 올바르게 학습하는 데 있어서 중요한 역할을 한다.
수치 미분
미분
미분은 한순간의 변화량을 표시한 것으로 수식은 다음과 같다.
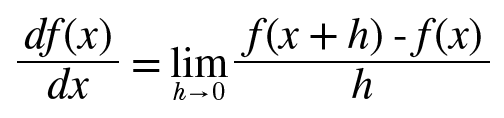
x의 작은 변화가 함수 f(x)를 얼마나 변화시키느냐를 의미한다. 이때 시작의 작은 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미를 lim h->0로 나타낸다. 파이썬으로 구현하면 다음과 같다.
def numerical_dff(f, x):
h = 1e-50
return (f(x + h) - f(x)) / h이 방식에는 두 가지 문제점이 있다.
첫 번째는 계산 오차에 관한 문제이다. h에 가급적 작은 값을 대입하고 싶었기에 1e-50이라는 작은 값을 이용했다. 하지만, 이 방식은 반올림 오차 문제를 일으킨다. 작은 값이 생략되어 최종 계산 결과에 오차가 생기는 문제점이다. 예를 들어, 파이썬에서는 1e-50을 float32형으로 나타내면 0.0이 되어 컴퓨터로 계산하는데 문제가 생긴다.
두 번째는 함수 f의 차분과 관련한 것이다. 진정한 미분은 x 위치의 함수의 기울기에 해당하지만, 이번 구현에서의 미분은 (x+h)와 x사이의 기울기에 해당한다. 이 차이는 h를 무한히 0으로 좁히는 것이 불가능해 생기는 한계이다.
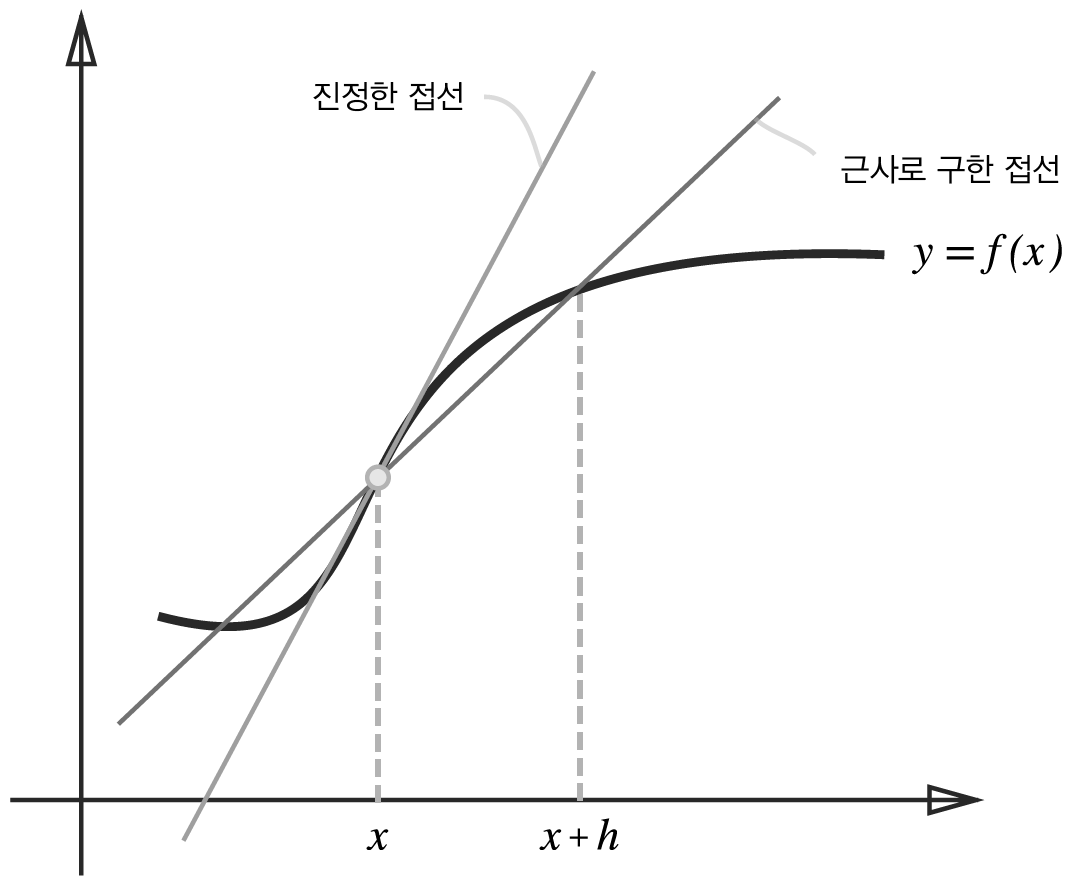
위 그림과 같이 수치 미분에는 오차가 포함된다. 이 오차를 줄이기 위해 (x+h)와 (x-h) 일 때의 함수 f의 차분을 계산하는 방법을 쓰기도 한다. 이 차분은 x를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분 혹은 중앙 차분이라고 한다. (x+h)와 x의 차분은 전방 차분이라고 한다. 이를 적용해 수치 미분을 다시 구현하면 다음과 같다.
def numerical_dff2(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / 2*h수치 미분의 예
다음과 같은 2차 함수가 있을 때 수치 미분을 사용해서 미분해 보자.
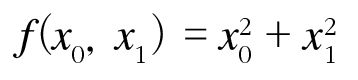
import numpy as np
import matplotlib.pylab as plt
def function_1(x):
return 0.001*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.show()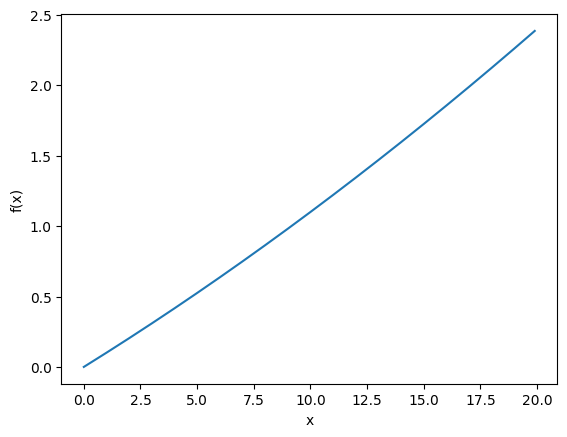
식 4.5와 5에서의 접선 그래프를 동시에 표현하면 다음과 같다.
def tangent_line(f, x):
d = numerical_diff(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = tangent_line(function_1, 5)
y2 = tf(x)
plt.plot(x, y)
plt.plot(x, y2)
plt.show()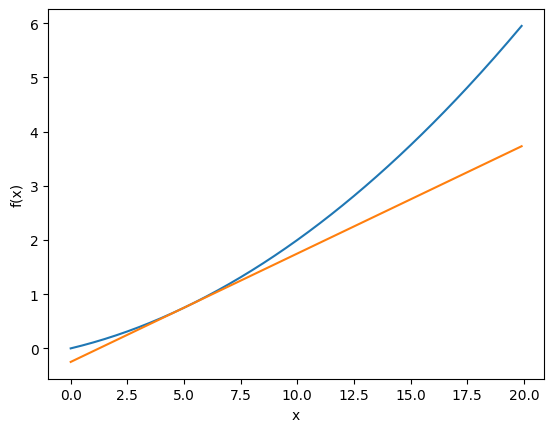
편미분
편미분은 인수들의 제곱 합을 계산하는 단순한 식이지만, 앞의 예와 달리 변수가 2개이다. 변수가 여럿인 함수에 대한 미분을 편미분이라고 한다.
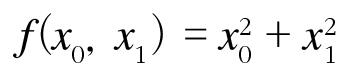
def function_2(x):
return x[0]**2 + x[1]**2
# 또는 return np.sum(x**2)편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다. 단, 여러 변수 중 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정한다.
'Books > 밑바닥부터 시작하는 딥러닝1' 카테고리의 다른 글
| [밑시딥1] Chapter4 신경망 학습(2) (0) | 2023.08.05 |
|---|---|
| [밑시딥1] Chapter3 신경망 (0) | 2023.08.05 |
| [밑시딥1] Chapter2 퍼셉트론 (0) | 2023.08.03 |
해당 포스팅은 <밑바닥부터 시작하는 딥러닝1> 책을 기준으로 하며, 공부 기록 목적으로 작성되었습니다.

학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻한다. 손실 함수는 신경망이 학습할 수 있도록 해주는 지표로 손실 함수의 결괏값을 가장 작게 만드는 개중치 매개변수를 찾는 것이 학습의 목표이다.
데이터에서 학습한다!
신경망의 특징은 데이터를 보고 학습할 수 있다는 점이고 학습한다는 것은 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 의미이다.
데이터 주도 학습
기계학습은 데이터에서 답과 패턴을 찾고 데이터로 이야기를 만드는 것이기 때문에 그 중심에는 데이터가 존재한다.
기계학습에서는 사람의 개입을 최소화하고 수집한 데이터로부터 패턴을 찾으려 시도한다. 신경망과 딥러닝은 기존 기계학습에서 사용하던 방법보다 사람의 개입을 더욱 배제할 수 있게 해주는 중요한 특정을 지녔다.
이미지에서 특징을 추출하고 그 특징의 패턴을 기계학습의 기술로 학습하는 방법이 있다. 여기서 말하는 특징은 입력 데이터에서 본질적인(중요한) 데이터를 정확하게 추출할 수 있도록 설계된 변환기를 가리킨다. 이미지의 특징은 보통 벡터로 기술하고, 컴퓨터 비전 분야에서는 SIFT, SURF, HOG 등의 특징을 많이 사용한다. 이런 특징을 사용하여 이미지 데이터를 벡터로 변환하고 변환된 벡터를 가지고 지도 학습 방식의 대표 분류 기법인 SVM, KNN 등으로 학습할 수 있다.
기계학습에서는 데이터로부터 규칙을 찾는 역할을 '기계'가 담당하지만, 이미지를 벡터로 변환할 때 사용하는 특징은 여전히 '사람'이 설계한다 문제에 적합한 특징을 쓰지 않으면 좋은 결과를 얻을 수 없다.

신경망은 이미지는 있는 그대로 학습하기 때문에 두 번째 접근 방식에서는 특징을 사람이 설계했지만, 신경망은 이미지에 포함된 중요한 특징까지도 기계가 스스로 학습한다.
훈련 데이터와 시험 데이터
기계학습 문제는 데이터를 훈련 데이터와 시험 데이터로 나눠 학습과 실험을 수행한다. 우선 훈련 데이터만 사용하여 학습하면서 최적의 매개변수를 찾고 시험 데이터를 사용하여 앞서 훈련한 모델의 실력을 평가한다.
훈련, 시험 데이터를 나누는 이유?
우리는 범용적으로 사용할 수 있는 모델을 원하는데 이 범용 능력을 제대로 평가하기 위해서 데이터를 분리하는 것이다.
범용 능력은 아직 보지 못한 데이터로 문제를 올바르게 풀어내는 능력으로 범용 능력 획득이 기계학습의 최종 목표이다.
한 데이터셋에만 지나치게 최적화된 상태를 오버피팅이라고 하는데, 오버피팅을 피하는 것이 기계학습의 중요한 과제 중 하나이다.
손실 함수
신경망 학습에서는 현재의 상태를 하나의 지표로 표현한다. 그리고 그 지표를 가장 좋게 만들어주는 가중치 매개변수의 값을 탐색한다. 신경망 학습에서 사용하는 지표를 손실함수라고 하며 일반적으로 오차제곱합과 교차 엔트로피 오차를 사용한다.
오차제곱합
가장 많이 쓰이는 손실 함수는 오차제곱합(sum of squares for error, SSE)으로 수식은 다음과 같다.
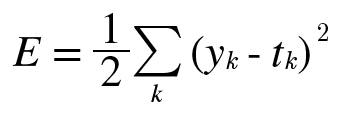
여기서 yk는 신경망의 출력(신경망이 추정한 값), tk는 정답 레이블, k는 데이터의 차원 수를 나타낸다. 신경망 출력 y는 소프트맥스 함수의 출력이 된다.
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)교차 엔트로피 오차
교차 엔트로피 오차(cross entropy error, CEE,)도 자주 이용한다. 수식은 다음과 같다.
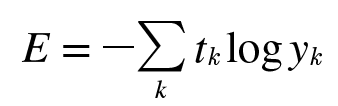
yk는 신경망 출력, tk는 정답 레이블이다. tk는 정답에 해당하는 인덱스의 원소만 1이고 나머지는 0이다(원-핫 인코딩). 실질적으로 정답일 때의 추정(tk가 1일 때의 yk)의 자연로그를 계산하는 식이 된다. 즉, 교차 엔트로피 오차는 정답일 때의 출력이 전체 값을 정하게 된다.

자연로그의 그래프는 위 그림에서 보듯이 x가 1일 때 y는 0이 되고 x가 0에 가까워질수록 y 값의 점점 작아진다. 교차 엔트로피 오차의 식도 마찬가지로 정답에 해당하는 출력이 커질수록 0에 다가가다가, 그 출력이 1일 때 0이 됩니다. 반대로 정답일 때의 출력이 작아질수록 오차는 커집니다.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))여기서 y와 t는 넘파이 배열이다. np.log() 함수에 0을 입력하면 마이너스 무한대를 뜻하는 -inf가 되어 더 이상 계산을 진행할 수 없게 되기 때문에 아주 작은 값 delta를 더에서 절대 0이 되지 않도록 했다.
미니배치 학습
기계학습 문제는 훈련 데이터를 사용해 학습하기 때문에 모든 훈련 데이터에 대해 손실 함수 값을 구해야 하고, 모든 손실 값의 합을 지표로 삼는다. 식은 다음과 같다.
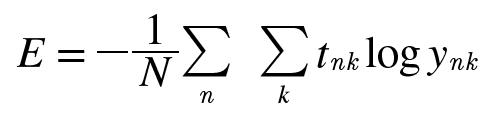
데이터가 N개라면 tnk는 n번째 데이터의 k번째 값을 의미한다(ynk는 신경망의 출력, tnk는 정답 레이블). 마지막에 N으로 나누어 정규화하고 있으며 N으로 나눔으로써 평균 손실 함수를 구한다.
데이터가 아주 많을 경우 데이터 일부를 추려 전체의 근사치로 이용할 수 있다. 신경망 학습에서도 훈련 데이터로부터 일부만 골라 학습을 수행하는데 이 일부를 미니배치라고 하고 이러한 학습 방법을 미니배치 학습이라고 한다.
훈련 데이터에서 지정한 수의 데이터를 무작위로 골라내는 코드는 다음과 같다.
import sys, os
sys.path.append("./dataset")
import numpy as np
import pickle
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize = False)
print(x_train.shape) # (60000, 784)
print(t_train.shape) # (60000,)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
np.random.choice(60000, 10)
# array([20705, 1907, 45562, 31219, 25882, 2401, 22636, 14447, 2463, 17281])손실 함수도 미니배치로 계산할 수 있다.
(배치용) 교차 엔트로피 오차 구현하기
미니배치 같은 배치 데이터를 지원하는 교차 엔트로피 오차는 아래 코드와 같이 구현할 수 있다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7) / batch_size)y는 신경망의 출력, t는 정답 레이블이다. y가 1차원이라면 즉, 데이터 하나당 교차 엔트로피 오차를 구하는 경우는 reshape 함수로 데이터의 형상을 바꿔준다. 그리고 배치의 크기로 나눠 정규화하고 이미지 1장 당 평균의 교차 엔트로피 오차를 계산한다.
정답 레이블이 원-핫 인코딩이 아니라 숫자 레이블로 주어졌을 때의 교차 엔트로피 오차는 다음과 같이 구현 가능하다.
def cross_entropy_error2(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y[np.arange(batch_size), t] + 1e-7) / batch_size)이 구현에서는 원-핫 인코딩일 때 t가 0인 원소는 교차 엔트로피 오차도 0이므로, 그 계산은 무시해도 좋다는 것이 핵심이다. 즉, 정답에 해당하는 신경망 출력만으로 교차 엔트로피 오차를 계산할 수 있다는 것이다.
왜 손실 함수를 설정하는가?
정확도라는 지표를 놔두고 손실 함수의 값이라는 우회적인 방법을 택하는 이유는 뭘까?
신경망 학습에서는 최적의 매개변수를 탐색할 때 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾는다. 이때 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다. 그러나 미분 값이 0이면 손실 함수의 값이 줄어들지 않고 가중치 매개변수의 갱신이 멈춘다. 정확도를 지표로 삼아서 안 되는 이유는 미분 값이 대부분의 장소에서 0이 되어 매개변수를 갱신할 수 없기 때문이다.
정확도는 매개변수의 미소한 변화에는 거의 반응을 보이지 않고, 반응이 있더라도 그 값이 불연속적으로 갑자기 변화한다.. 한편 손실 함수는 연속적으로 변화한다.
이는 계단 함수를 활성화 함수로 사용하지 않는 이유와도 들어맞는다. 매개변수의 작은 변화를 계단 함수가 말살하여 손실 함수의 값에 아무런 변화가 나타나지 않기 때문이다. 시그모이드 함수는 출력이 연속적이고 기울기도 연속적으로 변화하여 어느 장소를 미분해도 0이 되지 않는다. 이 성질이 신경망이 올바르게 학습하는 데 있어서 중요한 역할을 한다.
수치 미분
미분
미분은 한순간의 변화량을 표시한 것으로 수식은 다음과 같다.
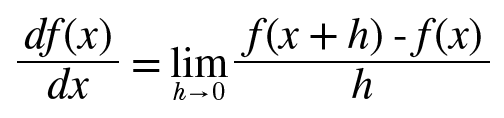
x의 작은 변화가 함수 f(x)를 얼마나 변화시키느냐를 의미한다. 이때 시작의 작은 변화, 즉 시간을 뜻하는 h를 한없이 0에 가깝게 한다는 의미를 lim h->0로 나타낸다. 파이썬으로 구현하면 다음과 같다.
def numerical_dff(f, x):
h = 1e-50
return (f(x + h) - f(x)) / h이 방식에는 두 가지 문제점이 있다.
첫 번째는 계산 오차에 관한 문제이다. h에 가급적 작은 값을 대입하고 싶었기에 1e-50이라는 작은 값을 이용했다. 하지만, 이 방식은 반올림 오차 문제를 일으킨다. 작은 값이 생략되어 최종 계산 결과에 오차가 생기는 문제점이다. 예를 들어, 파이썬에서는 1e-50을 float32형으로 나타내면 0.0이 되어 컴퓨터로 계산하는데 문제가 생긴다.
두 번째는 함수 f의 차분과 관련한 것이다. 진정한 미분은 x 위치의 함수의 기울기에 해당하지만, 이번 구현에서의 미분은 (x+h)와 x사이의 기울기에 해당한다. 이 차이는 h를 무한히 0으로 좁히는 것이 불가능해 생기는 한계이다.

위 그림과 같이 수치 미분에는 오차가 포함된다. 이 오차를 줄이기 위해 (x+h)와 (x-h) 일 때의 함수 f의 차분을 계산하는 방법을 쓰기도 한다. 이 차분은 x를 중심으로 그 전후의 차분을 계산한다는 의미에서 중심 차분 혹은 중앙 차분이라고 한다. (x+h)와 x의 차분은 전방 차분이라고 한다. 이를 적용해 수치 미분을 다시 구현하면 다음과 같다.
def numerical_dff2(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / 2*h수치 미분의 예
다음과 같은 2차 함수가 있을 때 수치 미분을 사용해서 미분해 보자.
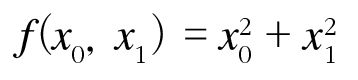
import numpy as np
import matplotlib.pylab as plt
def function_1(x):
return 0.001*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.show()
식 4.5와 5에서의 접선 그래프를 동시에 표현하면 다음과 같다.
def tangent_line(f, x):
d = numerical_diff(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
tf = tangent_line(function_1, 5)
y2 = tf(x)
plt.plot(x, y)
plt.plot(x, y2)
plt.show()
편미분
편미분은 인수들의 제곱 합을 계산하는 단순한 식이지만, 앞의 예와 달리 변수가 2개이다. 변수가 여럿인 함수에 대한 미분을 편미분이라고 한다.
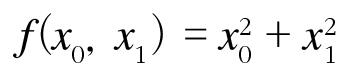
def function_2(x):
return x[0]**2 + x[1]**2
# 또는 return np.sum(x**2)편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다. 단, 여러 변수 중 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정한다.
'Books > 밑바닥부터 시작하는 딥러닝1' 카테고리의 다른 글
| [밑시딥1] Chapter4 신경망 학습(2) (0) | 2023.08.05 |
|---|---|
| [밑시딥1] Chapter3 신경망 (0) | 2023.08.05 |
| [밑시딥1] Chapter2 퍼셉트론 (0) | 2023.08.03 |
