논문 링크: https://arxiv.org/abs/1509.06461
강화학습은 에이전트가 환경과 상호작용하며 최적의 행동을 학습하는 방식으로,
DQN(Deep Q-Network)은 이를 딥러닝과 결합하여 고차원 상태 공간을 효과적으로 처리하고, experience replay와 target network를 통해 안정적인 학습을 가능하게 합니다.
그러나 DQN은 Q-value 추정 시 overestimate 문제와 학습 불안정하다는 등의 단점을 가지고 있습니다.
이를 해결하기 위해 Double DQN이 제안되었으며, 두 개의 Q-network를 활용하여 overestimate 문제를 완화하고 더욱 안정적인 학습을 가능하게 합니다. 이번 포스팅에서는 Double DQN을 다루고 있는 'Deep Reinforcement Learning with Double Q-learning' 논문에 대해서 정리 및 리뷰해 보도록 하겠습니다.
Abstract
Q-learning 알고리즘은 action values 값을 과대평가하는 경우가 있다. Q-learning에 deep neural network를 적용한 DQN 역시 일부 게임에서 같은 현상이 나타난다.
따라서, Double Q-learning의 알고리즘의 아이디어를 large-scale function approximation에도 일반화할 수 있음을 증명하며, 이를 이용한 Double DQN 알고리즘을 통해서 위에서 언급했던 과대평가 문제를 해결한다.
과대평가가 항상 나쁜 것은 아니지만, 균일하지 않거나 학습하고자 하는 상태에 집중되지 않으면, 결과 정책의 품질에 부정적인 영향을 미쳐서 결국 subobtimal 한 정책으로 이어질 수 있다고 한다.
논문에서는 Double-Q learning을 제시하며, 결과적으로 더 정확한 값 추정치를 산출할 뿐 아니라 여러 게임에서 훨씬 더 높은 점수를 이끌어냄을 확인한다.
Q-learning
q-learning은 $Q_{\pi}(s, a)$ 값이 다음과 같다고 할 때, state에서 q-value가 max 값이 선택함으로써 optimal policy를 도출하는 강화학습 알고리즘이다.
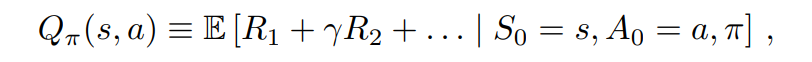
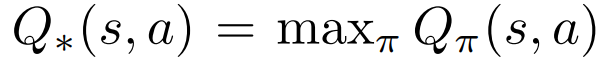
q-value를 매개변수화해서 $Q(s, a; \theta_t)$ 로 나타낸다고 할 때 q-learning 업데이트과정은 다음과 같다.
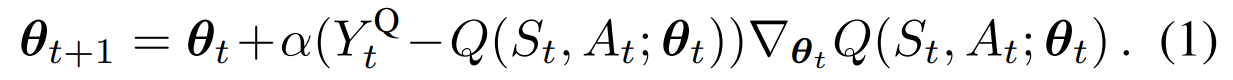
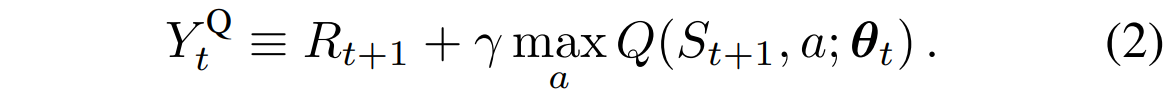
- $α$ : scalar step size
- $Y_t^Q$ : target value
업데이트 과정을 풀어서 설명하면
target value는 즉각적인 보상에 max인 action을 취했을 때의 q-value를 discount factor를 곱해서 나타낼 수 있고, 파라미터는 그 target value와 현재의 q-value를 뺀 값에 step size와 gradient를 곱한 값으로 업데이트를 진행한다.
Deep Q Networks
DQN은 다층 신경망으로 주어진 state $s$에 대해서 action value인 q-value $Q(s, \cdot; \theta)$ 를 출력하는 네트워크를 학습한다.
DQN에서 중요한 핵심 요소는 2가지가 있다.
- fixed target network의 사용: 매개변수를 가진 target network는 매 $\tau$ 스텝마다 매개변수가 복사되어 $\theta_{t^-} = \theta_t$ 가 되고, 다른 모든 단계에서는 고정된다.
- experience replay의 사용: 관찰된 transition은 일정 시간동안 replay buffer에 저장되고 buffer에서 무작위로 샘플링하여 네트워크를 업데이트한다.
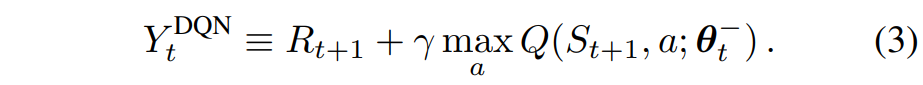
Double Q-learning
기존 q-learning이나 DQN에서는 action을 선택하고 평가하기 위해 동일한 값을 사용한다. 이는 과대평가된 값을 선택할 가능성을 높이고 overoptimistic value estimate를 초래한다.
이를 이해하기 쉽게 설명해보자면 다음과 같다.
에이전트가 상태 $s_1$에 있을 때, 가능한 action을 exploration을 통해 선택하고, 그 결과 다음 상태 $s_2$ 로 이동한다고 가정해 보자. $s_2$ 에서 에이전트는 해당 행동의 결과로 reward을 받는다. 이 reward이 매우 낮을 수 있다. 길을 안전하게 가야 하는 task에서 웅덩이에 빠진 것을 예로 들 수 있다.
q-learning 알고리즘은 다음 상태 $s_2$ 에서의 최대 q-value을 사용하여 상태 $s_1$ 에서의 q-value을 업데이트한다. 여기서 중요한 점은, 에이전트는 상태 $s_2$ 에서의 최악의 보상을 받았더라도, 다음 상태에서의 최대 q-value을 기준으로 현재 상태의 q-value을 조정한다는 것이다.
이 과정에서 에이전트는 상태 $s_1$ 근처에 존재하는 매우 안 좋은 상태를 과소평가할 가능성이 있다. 이는 상태 $s_1$ 의 q-value 이 실제로는 좋지 않은 상태임에도 불구하고, 다음 상태에서의 최대 q-value 을 참고하기 때문에 발생하는 문제이다. 결과적으로 상태 $s_1$ 의 q-value이 실제보다 과대평가될 수 있다.
이를 방지하기 위해서 action의 선택과 action value의 평가를 분리한 것이 double q-learning의 아이디어이다.
double q-learning 에서는 두 개의 value function 중에서 무작위로 하나를 선택해서 업데이트하도록 한다. 각 업데이트마다 하나의 value function을 선택해서 greedy policy를 결정하고, 다른 하나를 사용해서 그 value를 평가한다.
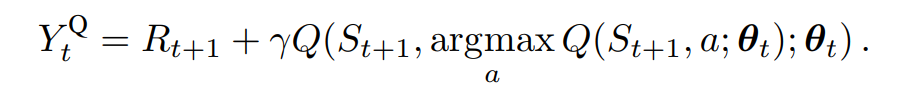
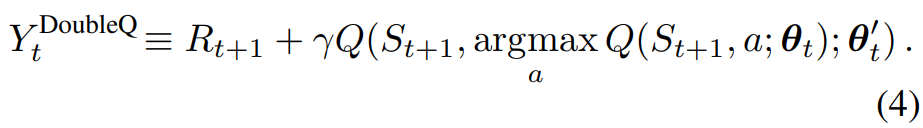
Overoptimism due to estimation errors
선행연구에 따르면 q-learning에서 overestimation이 결국 suboptimal policy로 이어진다고 한다.
이 섹션에서는 estimation error가 environmental noise, function approximation, non-stationarity 또는 다른 어떤 원인으로 인해 발생하든 상관없이 upward bias을 유발할 수 있음을 더 일반적으로 보여준다.
Theorem1.
모든 true optimal action values가 $Q^*(s, a) = V^*(s)$ 인 어떤 $V^*(s)$ 에 대해 동일한 상태 $s$를 고려해 보자. $Q_t$를 $\sum_a (Q_t(s, a) - V^*(s)) = 0$ 의 의미에서 전반적으로 편향되지 않았지만, 모두 정확하지는 않아서 $\frac{1}{m} \sum_a (Q_t(s, a) - V^*(s))^2 = C'$ 가 되는 임의의 값 추정치라고 하자. 여기서 $C' > 0$ 이고, $m \geq 2$ 는 $s$에서의 행동 수이다.
이러한 조건 하에서, $\max_a Q_t(s, a) \geq V^*(s) + \sqrt{\frac{C'}{m-1}}$. 이 하한은 엄격하다. 동일한 조건 하에서, Double Q-learning 추정치의 절대 오차에 대한 하한은 0이다. (증명은 부록에 있음.)
추정값들이 평균적으로는 정확하더라도, 일부 추정값은 실제 값보다 높을 수 있다.
Q-learning은 이 중 최대값을 선택하므로, 과대평가된 값을 선택할 가능성이 높아진다.
- 과대평가에 대한 수학적 하한선을 제시한다.
- 행동의 수가 많을수록 이 하한선은 낮아지지만, 실제로는 과대평가가 더 심해질 수 있다.
이 정리는 각 행동에 대한 추정 이 정리는 각 행동에 대한 추정 오차가 독립적일 필요가 없다는 점을 강조한다.
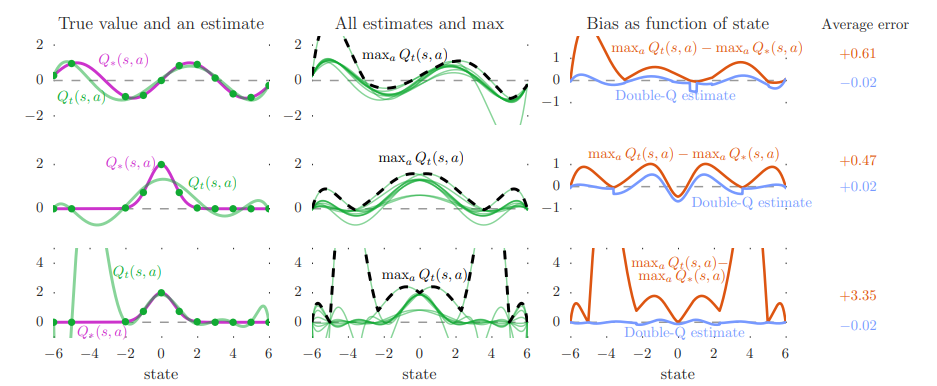
Figure 2에서는 강화학습 중 발생하는 overestimate을 시각적으로 보여준다. 실험 결과 그래프를 보면 Double DQN은 overestimate 문제를 줄여, 더 정확한 q-value을 추정할 수 있음을 확인할 수 있음을 확인할 수 있다.
- 실험 설정:
- 연속적인 state space, 각 state에 10개의 discrete action
- True optimal action value는 state에만 의존 (모든 action이 같은 value)
- True value function: $Q^*(s, a) = \sin(s)$ 또는 $Q^*(s, a) = 2 \exp(-s^2)$
- function approximation
- d차 다항식 사용 (d = 6 또는 d = 9)
- Sample은 노이즈 없이 true function과 정확히 일치
- 그래프 해석
- True value and an estimate
- 상위 두 행에서는 함수 근사가 충분히 유연하지 않아 sampled state에서도 근사가 정확하지 않고, 하단 행에서는 함수가 녹색 점에 맞출 만큼 유연하지만, 이로 인해 unsampled state에서의 정확도가 떨어진다.
- 왼쪽 plot의 왼쪽 부분에서 sampled state 간격이 더 넓어져 더 큰 estimation error가 발생함
- All estimates and max
- 대체적으로 추정된 maximum action value(검은 점선)가 ground truth보다 높음
- Bias as function of state
- 주황색 선이 q-learning과 ground truth와의 차이인데 대부분 양수이고 마지막은 unseen state에 대한 estimation error가 높아져 더 큰 과대 추정을 초래
- 파란색 선은 double q-learning을 사용했을 때의 estimate과 ground truth와의 차이인데 차이가 많이 준 것을 확인할 수 있음
- True value and an estimate
위에서 알 수 있는 사실은 q-learning의 과대 추정이 특정 함수의 결과가 아니다. 이때, 유연성이 높으면 unseen state에서 과대 추정 증가하게 되는데 유연한 parametric function approximator가 강화학습에서 자주 사용된다. 따라서, 과대 추정 문제가 실제 응용에서 중요한 이슈임을 시사하고 있다.
특히, 위의 예에서는 특정 state에서 true action value의 sample이 있다고 가정했음에도 과대 추정이 발생한다.
과대 추정과 bootstrapping의 결합은 어떤 state가 다른 state보다 더 가치 있는지에 대한 잘못된 상대적 정보를 전파하는 해로운 효과를 가져와 학습된 policy의 질에 직접적인 영향을 미친다. 논문에서 언급한 선행연구는 이러한 과대 추정이 실제로 optimal policy 학습을 방해할 수 있다고 지적했다.
논문에서는 이후의 실험에서 policy 품질에 대한 이러한 부정적인 영향을 확인하고 Double Q-learning을 사용하여 과대 추정을 줄여 policy를 개선한다.
Double DQN
Double Q-learning의 아이디어: target에서 max 연산을 행동 선택과 행동 평가로 분해하여 과대평가를 줄이는 것
Double DQN은 온라인 네트워크로 greedy policy을 평가하고, target network를 사용하여 그 가치를 추정한다. 이는 DQN과 동일하지만, target $Y_t^{DQN}$ 을 $Y_t^{DoubleDQN}$ 으로 교체한다.
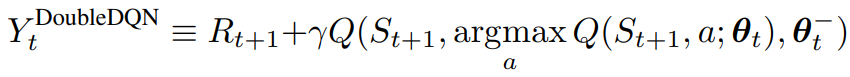
이때 식 (4)의 두 번째 네트워크의 가중치를 타겟 네트워크의 가중치로 대체하여 현재 탐욕 정책을 평가한다.
- 온라인 네트워크 $Q_{\theta}$ : 현재 학습 중인 네트워크로, 행동을 선택하는 데 사용
- 타겟 네트워크 $Q_{\theta^-}$ : 일정 간격으로 온라인 네트워크의 가중치를 복사하여 업데이트되는 네트워크로, 선택된 행동의 가치를 평가하는 데 사용
Empirical results
- DQN의 과대평가를 분석
- Double DQN이 값의 정확성과 정책 품질 모두에서 DQN보다 개선됨
- testbed: Atari 2600 게임으로 실험
- 입력이 고차원이면서, 게임의 시각적 요소와 게임 메커니즘이 게임마다 크게 다르기 때문에 매우 까다로움
- network architecture: 3개의 convolution layer, fc hidden layer (총 약 150만 개의 parameter)로 구성된 convolutional neural network
- input: 마지막 4개의 frame
- output: 각 action 값을 출력
- 각 게임에서 네트워크는 단일 GPU에서 2억 frames, 약 1주일 동안 학습
Results on overoptimism
Figure 3에서는 여섯 개의 Atari 게임에서 DQN의 과대평가 예시를 보여준다.
- 주황색: DQN
- 파란색: DDQN
- T=125,000
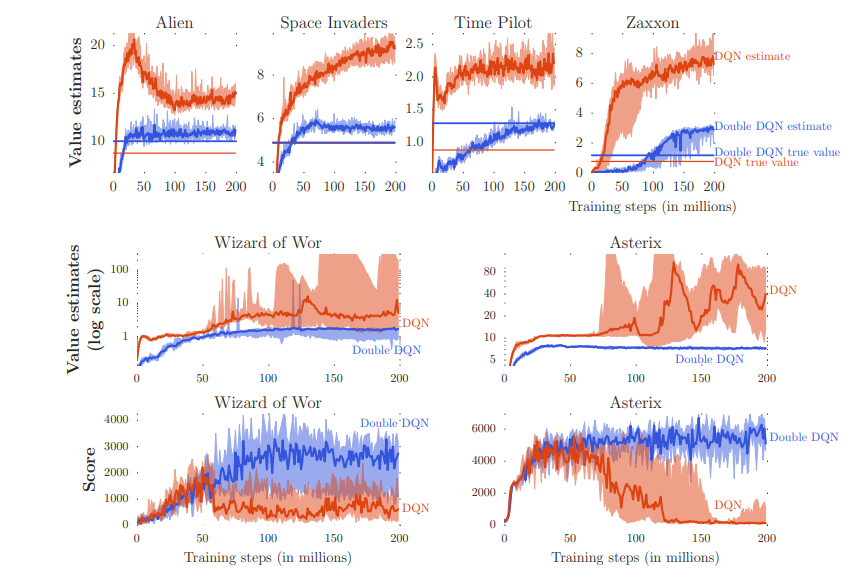
DQN이 일관되게 value를 과대평가하는 경향이 있으며, 성능을 측정하면 DDQN이 더 높게 측정되는 것을 확인할 수 있다. 즉, DDQN이 더 정확한 값 추정치를 제공할 뿐만 아니라 더 나은 정책을 생성한다는 것을 보여준다.
Quality of the learned policies
DQN이 테스트된 49개 게임 모두에서 정책 품질 측면에서 Double DQN이 얼마나 도움이 되는지 더 일반적으로 평가한다.
evaluation
- 각 evaluation 에피소드는 최대 30회까지 환경에 영향을 주지 않는 특별한 no-op action을 실행하여 에이전트에게 다른 시작점을 제공하는 것으로 시작
- 일부 exploration은 추가적인 randomization 제공
- Double DQN의 경우, DQN과 동일한 하이퍼파라미터를 사용
- 5분의 에뮬레이터 시간(18,000 프레임) 동안 $\epsilon = 0.05$ 인 $\epsilon$ - greedy policy으로 평가
- 점수: 100 에피소드 평균

Robustness to Human starts
다양한 시작 지점에서 에이전트를 테스트함으로써, 솔루션이 잘 일반화되는지 테스트를 진행하였다.
tuning version
- the target network 업데이트를 10,000 프레임마다 하는 것에서 30,000 프레임마다 하는 것으로 변경
- 온라인 네트워크의 안정성을 높여서 Q-learning으로의 급격한 전환을 줄여주기 위해
- 또한 학습 중 exploration을 $\epsilon = 0.1 \rightarrow \epsilon = 0.01$, 평가 중에는 $\epsilon = 0.001$
- uses a single shared bias for all action values in the top layer of the network
- 매개변수 수가 줄어들어 모델이 더 간결해지고, 학습이 더 효율적으로 이루어질 수 있음
- 학습 과정에서 일관성이 유지되어 모델이 overfitting 되는 것을 방지하고, 더 일반화된 성능을 발휘할 수 있도록 도와줌

DQN, Double DQN, Tuning version의 Double DQN 비교 결과는 다음 그래프에서 확인할 수 있다.
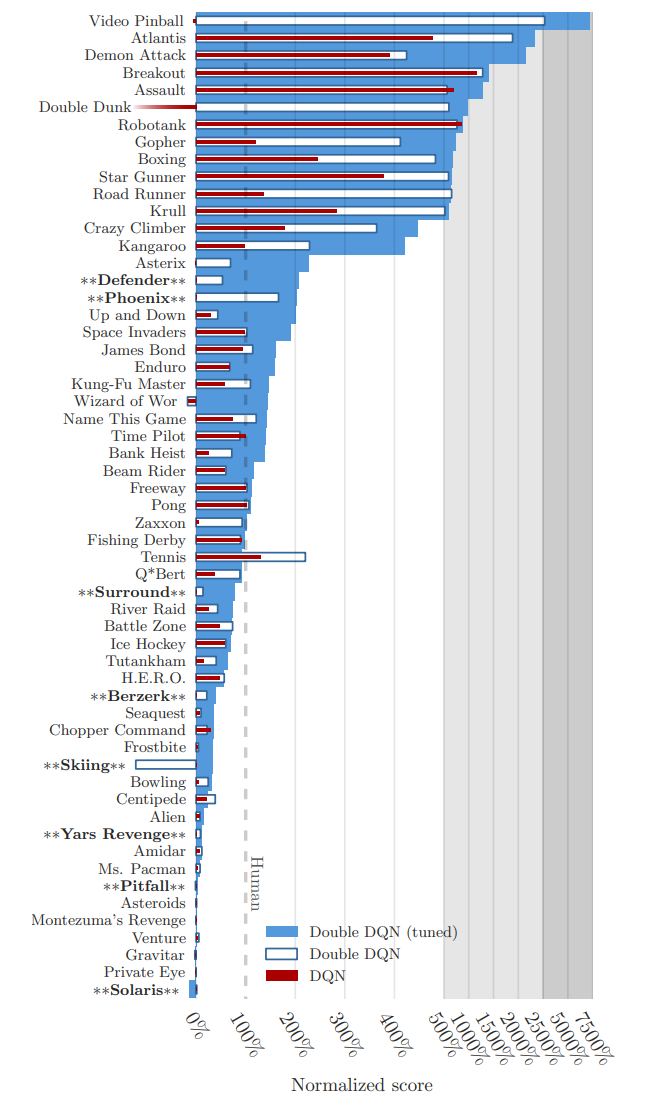
Discussion
논문에서는 다음과 같이 5가지로 contribution을 정리하고 있다.
- 대규모 문제에서 Q-learning이 지나치게 낙관적일 수 있는 이유 입증
- Atari 게임에 대한 value estimates를 분석하여 이러한 과대추정이 이전에 알려진 것보다 실제로는 더 일반적이고 심각하다는 것을 보여줌
- Double Q-learning을 대규모로 사용하면 이러한 overoptimism를 성공적으로 줄여 보다 안정적이고 신뢰할 수 있는 학습을 할 수 있음을 보여줌
- 추가 네트워크나 매개변수 없이 DQN의 기존 아키텍처와 심층 신경망을 사용하는 Double DQN이라는 구체적인 구현을 제안
- Double DQN이 더 나은 policy를 찾아내어 Atari 2600 도메인에서 sota 달성
'ML & DL > RL' 카테고리의 다른 글
| [RL] 강화학습 REINFORCE 알고리즘 (0) | 2024.07.31 |
|---|---|
| [RL] 강화학습 Policy Gradient 수식 전개 (0) | 2024.07.31 |
| [RL] 강화학습 Policy-based 개념 간단 정리 (0) | 2024.07.31 |
| [RL] 간단하게 정리한 On-policy, Off-policy, Online, Offline Reinforcement Learning (0) | 2024.06.13 |
| [RL] 강화학습이란 (0) | 2023.09.06 |
논문 링크: https://arxiv.org/abs/1509.06461
강화학습은 에이전트가 환경과 상호작용하며 최적의 행동을 학습하는 방식으로,
DQN(Deep Q-Network)은 이를 딥러닝과 결합하여 고차원 상태 공간을 효과적으로 처리하고, experience replay와 target network를 통해 안정적인 학습을 가능하게 합니다.
그러나 DQN은 Q-value 추정 시 overestimate 문제와 학습 불안정하다는 등의 단점을 가지고 있습니다.
이를 해결하기 위해 Double DQN이 제안되었으며, 두 개의 Q-network를 활용하여 overestimate 문제를 완화하고 더욱 안정적인 학습을 가능하게 합니다. 이번 포스팅에서는 Double DQN을 다루고 있는 'Deep Reinforcement Learning with Double Q-learning' 논문에 대해서 정리 및 리뷰해 보도록 하겠습니다.
Abstract
Q-learning 알고리즘은 action values 값을 과대평가하는 경우가 있다. Q-learning에 deep neural network를 적용한 DQN 역시 일부 게임에서 같은 현상이 나타난다.
따라서, Double Q-learning의 알고리즘의 아이디어를 large-scale function approximation에도 일반화할 수 있음을 증명하며, 이를 이용한 Double DQN 알고리즘을 통해서 위에서 언급했던 과대평가 문제를 해결한다.
과대평가가 항상 나쁜 것은 아니지만, 균일하지 않거나 학습하고자 하는 상태에 집중되지 않으면, 결과 정책의 품질에 부정적인 영향을 미쳐서 결국 subobtimal 한 정책으로 이어질 수 있다고 한다.
논문에서는 Double-Q learning을 제시하며, 결과적으로 더 정확한 값 추정치를 산출할 뿐 아니라 여러 게임에서 훨씬 더 높은 점수를 이끌어냄을 확인한다.
Q-learning
q-learning은 $Q_{\pi}(s, a)$ 값이 다음과 같다고 할 때, state에서 q-value가 max 값이 선택함으로써 optimal policy를 도출하는 강화학습 알고리즘이다.
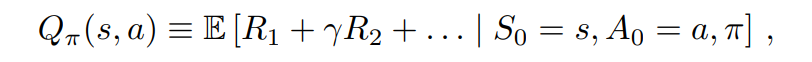
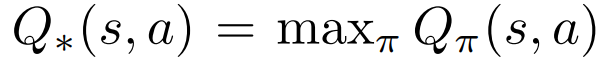
q-value를 매개변수화해서 $Q(s, a; \theta_t)$ 로 나타낸다고 할 때 q-learning 업데이트과정은 다음과 같다.
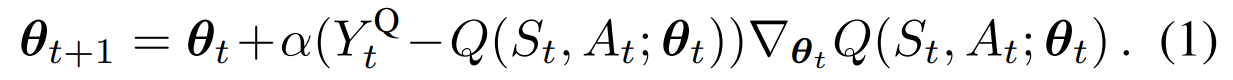
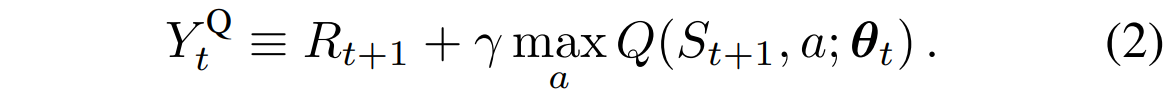
- $α$ : scalar step size
- $Y_t^Q$ : target value
업데이트 과정을 풀어서 설명하면
target value는 즉각적인 보상에 max인 action을 취했을 때의 q-value를 discount factor를 곱해서 나타낼 수 있고, 파라미터는 그 target value와 현재의 q-value를 뺀 값에 step size와 gradient를 곱한 값으로 업데이트를 진행한다.
Deep Q Networks
DQN은 다층 신경망으로 주어진 state $s$에 대해서 action value인 q-value $Q(s, \cdot; \theta)$ 를 출력하는 네트워크를 학습한다.
DQN에서 중요한 핵심 요소는 2가지가 있다.
- fixed target network의 사용: 매개변수를 가진 target network는 매 $\tau$ 스텝마다 매개변수가 복사되어 $\theta_{t^-} = \theta_t$ 가 되고, 다른 모든 단계에서는 고정된다.
- experience replay의 사용: 관찰된 transition은 일정 시간동안 replay buffer에 저장되고 buffer에서 무작위로 샘플링하여 네트워크를 업데이트한다.
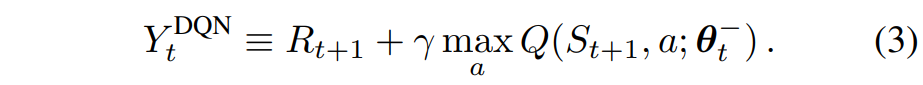
Double Q-learning
기존 q-learning이나 DQN에서는 action을 선택하고 평가하기 위해 동일한 값을 사용한다. 이는 과대평가된 값을 선택할 가능성을 높이고 overoptimistic value estimate를 초래한다.
이를 이해하기 쉽게 설명해보자면 다음과 같다.
에이전트가 상태 $s_1$에 있을 때, 가능한 action을 exploration을 통해 선택하고, 그 결과 다음 상태 $s_2$ 로 이동한다고 가정해 보자. $s_2$ 에서 에이전트는 해당 행동의 결과로 reward을 받는다. 이 reward이 매우 낮을 수 있다. 길을 안전하게 가야 하는 task에서 웅덩이에 빠진 것을 예로 들 수 있다.
q-learning 알고리즘은 다음 상태 $s_2$ 에서의 최대 q-value을 사용하여 상태 $s_1$ 에서의 q-value을 업데이트한다. 여기서 중요한 점은, 에이전트는 상태 $s_2$ 에서의 최악의 보상을 받았더라도, 다음 상태에서의 최대 q-value을 기준으로 현재 상태의 q-value을 조정한다는 것이다.
이 과정에서 에이전트는 상태 $s_1$ 근처에 존재하는 매우 안 좋은 상태를 과소평가할 가능성이 있다. 이는 상태 $s_1$ 의 q-value 이 실제로는 좋지 않은 상태임에도 불구하고, 다음 상태에서의 최대 q-value 을 참고하기 때문에 발생하는 문제이다. 결과적으로 상태 $s_1$ 의 q-value이 실제보다 과대평가될 수 있다.
이를 방지하기 위해서 action의 선택과 action value의 평가를 분리한 것이 double q-learning의 아이디어이다.
double q-learning 에서는 두 개의 value function 중에서 무작위로 하나를 선택해서 업데이트하도록 한다. 각 업데이트마다 하나의 value function을 선택해서 greedy policy를 결정하고, 다른 하나를 사용해서 그 value를 평가한다.
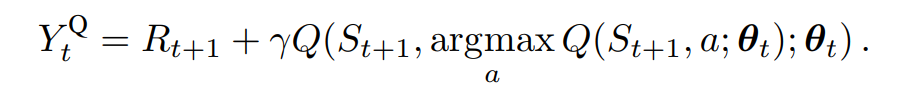
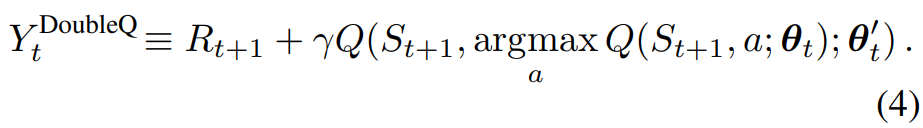
Overoptimism due to estimation errors
선행연구에 따르면 q-learning에서 overestimation이 결국 suboptimal policy로 이어진다고 한다.
이 섹션에서는 estimation error가 environmental noise, function approximation, non-stationarity 또는 다른 어떤 원인으로 인해 발생하든 상관없이 upward bias을 유발할 수 있음을 더 일반적으로 보여준다.
Theorem1.
모든 true optimal action values가 $Q^*(s, a) = V^*(s)$ 인 어떤 $V^*(s)$ 에 대해 동일한 상태 $s$를 고려해 보자. $Q_t$를 $\sum_a (Q_t(s, a) - V^*(s)) = 0$ 의 의미에서 전반적으로 편향되지 않았지만, 모두 정확하지는 않아서 $\frac{1}{m} \sum_a (Q_t(s, a) - V^*(s))^2 = C'$ 가 되는 임의의 값 추정치라고 하자. 여기서 $C' > 0$ 이고, $m \geq 2$ 는 $s$에서의 행동 수이다.
이러한 조건 하에서, $\max_a Q_t(s, a) \geq V^*(s) + \sqrt{\frac{C'}{m-1}}$. 이 하한은 엄격하다. 동일한 조건 하에서, Double Q-learning 추정치의 절대 오차에 대한 하한은 0이다. (증명은 부록에 있음.)
추정값들이 평균적으로는 정확하더라도, 일부 추정값은 실제 값보다 높을 수 있다.
Q-learning은 이 중 최대값을 선택하므로, 과대평가된 값을 선택할 가능성이 높아진다.
- 과대평가에 대한 수학적 하한선을 제시한다.
- 행동의 수가 많을수록 이 하한선은 낮아지지만, 실제로는 과대평가가 더 심해질 수 있다.
이 정리는 각 행동에 대한 추정 이 정리는 각 행동에 대한 추정 오차가 독립적일 필요가 없다는 점을 강조한다.
Figure 2에서는 강화학습 중 발생하는 overestimate을 시각적으로 보여준다. 실험 결과 그래프를 보면 Double DQN은 overestimate 문제를 줄여, 더 정확한 q-value을 추정할 수 있음을 확인할 수 있음을 확인할 수 있다.

- 실험 설정:
- 연속적인 state space, 각 state에 10개의 discrete action
- True optimal action value는 state에만 의존 (모든 action이 같은 value)
- True value function: $Q^*(s, a) = \sin(s)$ 또는 $Q^*(s, a) = 2 \exp(-s^2)$
- function approximation
- d차 다항식 사용 (d = 6 또는 d = 9)
- Sample은 노이즈 없이 true function과 정확히 일치
- 그래프 해석
- True value and an estimate
- 상위 두 행에서는 함수 근사가 충분히 유연하지 않아 sampled state에서도 근사가 정확하지 않고, 하단 행에서는 함수가 녹색 점에 맞출 만큼 유연하지만, 이로 인해 unsampled state에서의 정확도가 떨어진다.
- 왼쪽 plot의 왼쪽 부분에서 sampled state 간격이 더 넓어져 더 큰 estimation error가 발생함
- All estimates and max
- 대체적으로 추정된 maximum action value(검은 점선)가 ground truth보다 높음
- Bias as function of state
- 주황색 선이 q-learning과 ground truth와의 차이인데 대부분 양수이고 마지막은 unseen state에 대한 estimation error가 높아져 더 큰 과대 추정을 초래
- 파란색 선은 double q-learning을 사용했을 때의 estimate과 ground truth와의 차이인데 차이가 많이 준 것을 확인할 수 있음
- True value and an estimate
위에서 알 수 있는 사실은 q-learning의 과대 추정이 특정 함수의 결과가 아니다. 이때, 유연성이 높으면 unseen state에서 과대 추정 증가하게 되는데 유연한 parametric function approximator가 강화학습에서 자주 사용된다. 따라서, 과대 추정 문제가 실제 응용에서 중요한 이슈임을 시사하고 있다.
특히, 위의 예에서는 특정 state에서 true action value의 sample이 있다고 가정했음에도 과대 추정이 발생한다.
과대 추정과 bootstrapping의 결합은 어떤 state가 다른 state보다 더 가치 있는지에 대한 잘못된 상대적 정보를 전파하는 해로운 효과를 가져와 학습된 policy의 질에 직접적인 영향을 미친다. 논문에서 언급한 선행연구는 이러한 과대 추정이 실제로 optimal policy 학습을 방해할 수 있다고 지적했다.
논문에서는 이후의 실험에서 policy 품질에 대한 이러한 부정적인 영향을 확인하고 Double Q-learning을 사용하여 과대 추정을 줄여 policy를 개선한다.
Double DQN
Double Q-learning의 아이디어: target에서 max 연산을 행동 선택과 행동 평가로 분해하여 과대평가를 줄이는 것
Double DQN은 온라인 네트워크로 greedy policy을 평가하고, target network를 사용하여 그 가치를 추정한다. 이는 DQN과 동일하지만, target $Y_t^{DQN}$ 을 $Y_t^{DoubleDQN}$ 으로 교체한다.
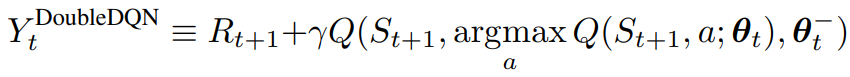
이때 식 (4)의 두 번째 네트워크의 가중치를 타겟 네트워크의 가중치로 대체하여 현재 탐욕 정책을 평가한다.
- 온라인 네트워크 $Q_{\theta}$ : 현재 학습 중인 네트워크로, 행동을 선택하는 데 사용
- 타겟 네트워크 $Q_{\theta^-}$ : 일정 간격으로 온라인 네트워크의 가중치를 복사하여 업데이트되는 네트워크로, 선택된 행동의 가치를 평가하는 데 사용
Empirical results
- DQN의 과대평가를 분석
- Double DQN이 값의 정확성과 정책 품질 모두에서 DQN보다 개선됨
- testbed: Atari 2600 게임으로 실험
- 입력이 고차원이면서, 게임의 시각적 요소와 게임 메커니즘이 게임마다 크게 다르기 때문에 매우 까다로움
- network architecture: 3개의 convolution layer, fc hidden layer (총 약 150만 개의 parameter)로 구성된 convolutional neural network
- input: 마지막 4개의 frame
- output: 각 action 값을 출력
- 각 게임에서 네트워크는 단일 GPU에서 2억 frames, 약 1주일 동안 학습
Results on overoptimism
Figure 3에서는 여섯 개의 Atari 게임에서 DQN의 과대평가 예시를 보여준다.
- 주황색: DQN
- 파란색: DDQN
- T=125,000

DQN이 일관되게 value를 과대평가하는 경향이 있으며, 성능을 측정하면 DDQN이 더 높게 측정되는 것을 확인할 수 있다. 즉, DDQN이 더 정확한 값 추정치를 제공할 뿐만 아니라 더 나은 정책을 생성한다는 것을 보여준다.
Quality of the learned policies
DQN이 테스트된 49개 게임 모두에서 정책 품질 측면에서 Double DQN이 얼마나 도움이 되는지 더 일반적으로 평가한다.
evaluation
- 각 evaluation 에피소드는 최대 30회까지 환경에 영향을 주지 않는 특별한 no-op action을 실행하여 에이전트에게 다른 시작점을 제공하는 것으로 시작
- 일부 exploration은 추가적인 randomization 제공
- Double DQN의 경우, DQN과 동일한 하이퍼파라미터를 사용
- 5분의 에뮬레이터 시간(18,000 프레임) 동안 $\epsilon = 0.05$ 인 $\epsilon$ - greedy policy으로 평가
- 점수: 100 에피소드 평균

Robustness to Human starts
다양한 시작 지점에서 에이전트를 테스트함으로써, 솔루션이 잘 일반화되는지 테스트를 진행하였다.
tuning version
- the target network 업데이트를 10,000 프레임마다 하는 것에서 30,000 프레임마다 하는 것으로 변경
- 온라인 네트워크의 안정성을 높여서 Q-learning으로의 급격한 전환을 줄여주기 위해
- 또한 학습 중 exploration을 $\epsilon = 0.1 \rightarrow \epsilon = 0.01$, 평가 중에는 $\epsilon = 0.001$
- uses a single shared bias for all action values in the top layer of the network
- 매개변수 수가 줄어들어 모델이 더 간결해지고, 학습이 더 효율적으로 이루어질 수 있음
- 학습 과정에서 일관성이 유지되어 모델이 overfitting 되는 것을 방지하고, 더 일반화된 성능을 발휘할 수 있도록 도와줌

DQN, Double DQN, Tuning version의 Double DQN 비교 결과는 다음 그래프에서 확인할 수 있다.

Discussion
논문에서는 다음과 같이 5가지로 contribution을 정리하고 있다.
- 대규모 문제에서 Q-learning이 지나치게 낙관적일 수 있는 이유 입증
- Atari 게임에 대한 value estimates를 분석하여 이러한 과대추정이 이전에 알려진 것보다 실제로는 더 일반적이고 심각하다는 것을 보여줌
- Double Q-learning을 대규모로 사용하면 이러한 overoptimism를 성공적으로 줄여 보다 안정적이고 신뢰할 수 있는 학습을 할 수 있음을 보여줌
- 추가 네트워크나 매개변수 없이 DQN의 기존 아키텍처와 심층 신경망을 사용하는 Double DQN이라는 구체적인 구현을 제안
- Double DQN이 더 나은 policy를 찾아내어 Atari 2600 도메인에서 sota 달성
'ML & DL > RL' 카테고리의 다른 글
| [RL] 강화학습 REINFORCE 알고리즘 (0) | 2024.07.31 |
|---|---|
| [RL] 강화학습 Policy Gradient 수식 전개 (0) | 2024.07.31 |
| [RL] 강화학습 Policy-based 개념 간단 정리 (0) | 2024.07.31 |
| [RL] 간단하게 정리한 On-policy, Off-policy, Online, Offline Reinforcement Learning (0) | 2024.06.13 |
| [RL] 강화학습이란 (0) | 2023.09.06 |
